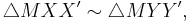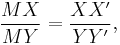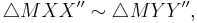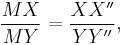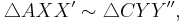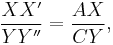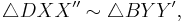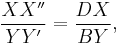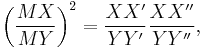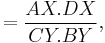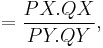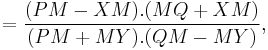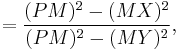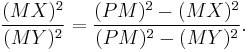Butterfly theorem
For the "butterfly lemma" of group theory, see Zassenhaus lemma.
The butterfly theorem is a classical result in Euclidean geometry, which can be stated as follows:
Let M be the midpoint of a chord PQ of a circle, through which two other chords AB and CD are drawn; AD and BC intersect chord PQ at X and Y correspondingly. Then M is the midpoint of XY.
A formal proof of the theorem is as follows: Let the perpendiculars  and
and  be dropped from the point
be dropped from the point 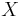 on the straight lines
on the straight lines 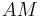 and
and 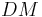 respectively. Similarly, let
respectively. Similarly, let 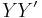 and
and 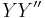 be dropped from the point
be dropped from the point 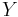 perpendicular to the straight lines
perpendicular to the straight lines 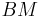 and
and 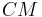 respectively.
respectively.
Now, since
From the preceding equations, it can be easily seen that
since 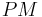 =
= 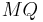
Now,
So, it can be concluded that 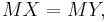 or
or 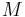 is the midpoint of
is the midpoint of 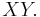
Bibliography
H. S. M. Coxeter, S. L. Greitzer, Geometry Revisited, MAA, 1967.
External links
- The Butterfly Theorem at cut-the-knot
- A Better Butterfly Theorem at cut-the-knot
- Proof of Butterfly Theorem at PlanetMath
- The Butterfly Theorem by Jay Warendorff, the Wolfram Demonstrations Project.
- Weisstein, Eric W., "Butterfly Theorem" from MathWorld.